PID valdikliai naudojami tam tikriems matuojamiesiems dydžiams paveikti. Kaip išmanūs „3-in-1“ valdikliai jie kasdien pasiteisina daugelyje pramoninių sistemų ir labai tiksliai valdo iki užduotosios vertės. Pateikiame jums svarbiausius faktus ir skaičius apie PID reguliavimą.
Kompaktiškas valdiklis gali būti pritaikytas įvairiems taikymams ir paprastai naudojamas kaip PID valdiklis. Jis veikia proporcingai, integruojant ir diferencijuojant (PID). Šiuo atveju atskirų komponentų intensyvumas pritaikomas prie valdymo proceso. Tai daroma nustatant valdymo parametrų matmenis
PID reguliatoriaus veikimo principą paaiškinti gana paprasta. Nesvarbu, ar tai būtų PID temperatūros, ar PID drėgmės valdiklis, valdiklis visada bando sureguliuoti konkretų valdymo kintamąjį iki užduotosios vertės, remdamasis faktine verte. Šiuo atveju P komponentas sustiprina valdymo nuokrypį, I komponentas padidina išėjimo lygį esant esamam valdymo nuokrypiui, o D komponentas neutralizuoja faktinės vertės judėjimą. Valdymui nereikalingus komponentus galima išjungti. Tada, priklausomai nuo taikymo srities, jie veikia kaip PI valdikliai, P valdikliai, PD valdikliai arba I valdikliai.
PID struktūra rodo geriausią valdymo reakciją daugumoje taikomųjų programų. Todėl kompaktiški PID valdikliai labai paplitę temperatūros reguliavimo srityje. Prie jų taip pat galima tiesiogiai prijungti RTD temperatūros zondus ir termoporas. Kai kuriems valdomiems kintamiesiems reikia išjungti tam tikrus komponentus, įskaitant greitį ir srautą.
P komponentas reaguoja labai greitai ir sustiprina valdymo skirtumą; jo nuolatinis valdymo nuokrypis turi neigiamą poveikį.Atsakingas valdymo parametras yra proporcinė juosta Pb.Esant mažesniems Pb matmenims, valdiklis tampa greitesnis, o valdymo nuokrypis mažesnis.Tačiau bendra sistema vis labiau linkusi svyruoti.
I komponentas pašalina valdymo nuokrypį. Jei nustatoma mažesnė atstatymo trukmė rt, valdiklis greičiau sukuria išėjimo lygį ir taip pat greičiau neutralizuoja valdymo nuokrypį. Tačiau jei nustatymas per mažas, taip pat atsiras svyravimų.
D komponentas neutralizuoja faktinės vertės pokytį. Šildymo valdikliui tai reiškia, kad komponentė mažėja, kai faktinė vertė didėja, ir didėja, kai faktinė vertė mažėja. Aprašyta elgsena turi slopinamąjį poveikį. Atsakingas parametras yra išvestinės laikas dt. Kuo didesnis dt nustatytas, tuo didesnis aprašytas poveikis.
Valdymo proceso elgsena visada priklauso nuo darbinio taško. Todėl prieš derinant įrenginys turi būti nustatytas į tokią darbinę būseną, kuriai vėliau tikimasi palankių valdymo parametrų. Pavyzdžiui, prieš derinant reikia pakrauti krosnį arba sukurti srautinio šildytuvo poreikį. Jei derinant reikia nurodyti užduotąją vertę, ji turėtų būti vėlesniame darbiniame diapazone.
Jei yra panašių įrenginių / valdymo kontūrų, juose naudojamus valdymo parametrus galima naudoti bandomuoju būdu. Jei šis metodas nepadeda pasiekti tikslo, galima taikyti vieną iš toliau nurodytų optimizavimo metodų.
Svyravimo metodas pagal Zieglerį ir Nicholsą
Šis metodas taikomas palyginti greitai valdomoms sistemoms. Paruošti, P struktūra parametrizuojama ir nustatomas santykinai didelis Pb. Toliau pateiktame paveikslėlyje apibrėžiama tolesniame darbiniame diapazone esanti užduotosios vertės reikšmė.
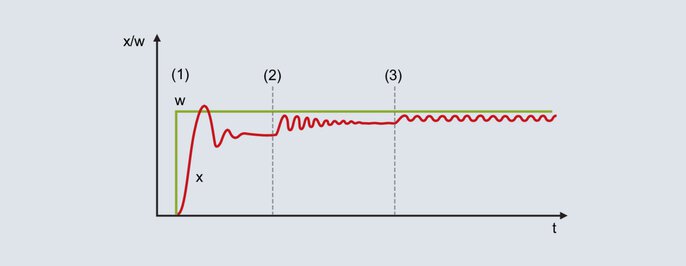
52 pav.: Nustatytosios ir faktinės vertės kreivė, kai naudojamas svyravimo metodas
Nustačius santykinai didelę proporcinę juostą, faktinė vertė juda link galutinės vertės su nedidele svyravimo tendencija [52 (1) paveikslas]. Dėl neegzistuojančios I struktūros atsiranda nuolatinis valdymo nuokrypis.
Pb sumažinama (52 pav. [2]): faktinė vertė padidėja ir juda prie galutinės vertės su didesniu polinkiu į svyravimus. Tam tikromis aplinkybėmis proporcinė juosta mažinama kelis kartus, kol faktinė vertė nuolat svyruoja (52 pav. [3]). Tokiam elgesiui reikalinga proporcinė juosta vadinama Pbc (kritinė Pb) ir turi būti nustatyta kuo tiksliau (nemažinkite Pb pernelyg dideliais žingsniais).
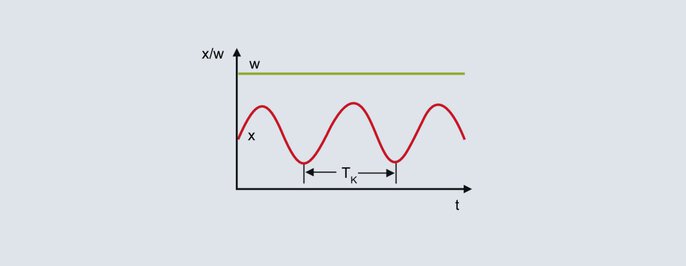
Kritinis laikotarpis
Iš viršutiniame paveikslėlyje pavaizduoto nuolatinio faktinės vertės svyravimo matyti, kad kritinio periodo trukmė Tc yra antrasis metodą apibūdinantis parametras, kurį reikia nustatyti. Kritinio periodo trukmė Tc (sekundėmis) apskaičiuojama pagal laiko intervalą tarp 2 mažiausių verčių, pvz. Siekiant nustatyti valdymo parametrus, Pbc ir Tc įrašomi į toliau pateiktą lentelę, skirtą numatytai valdiklio struktūrai:
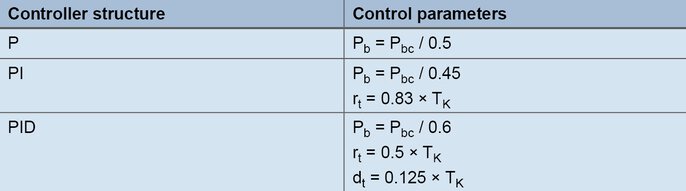
Nustatymo pagal svyravimo metodą formulės
Chieno, Hroneso ir Reswicko metodas, pagrįstas proceso etapo atsaku pagal Chieną, Hronesą ir Reswicką
Taikant šį metodą galima palyginti greitai įvertinti valdymo parametrus net ir lėtų valdymo procesų atveju. Metodas taikomas procesams nuo antros eilės ir pasižymi pereinamojo ir trikdžių elgsenos formulių išskyrimu. Taisyklių atveju valdymo proceso perdavimo koeficientas, uždelsimo laikas ir kompensavimo laikas apskaičiuojami remiantis žingsniniu atsaku.
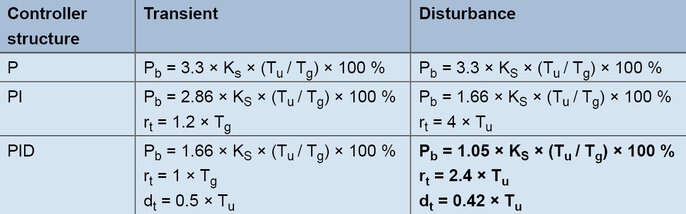
Sukūrimo pagal linijos žingsnio atsaką formulės
PID struktūros valdiklis turi būti naudojamas laboratorinei krosniai. Siekiama užtikrinti gerą elgesį esant trikdžiams, o tipinės užduotosios vertės yra 200 °C. Išėjimo lygis palaipsniui didinamas rankiniu režimu, kol faktinė vertė bus šiek tiek mažesnė už būsimąją užduotąją vertę (laukiama atitinkamų kompensavimo procesų). Pavyzdžiui, 180 °C temperatūra pasiekiama esant 60 % išėjimo lygiui. Pradedant nuo 60 %, išėjimo lygis staiga padidinamas iki 80 % ir užrašoma faktinė vertė.
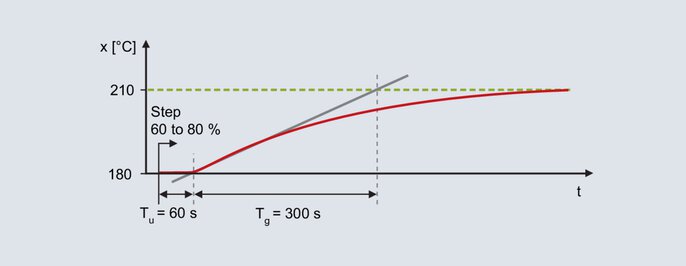
Laboratorinės krosnies žingsninė reakcija
Iš žingsnio atsako nustatymas vyksta naudojant išlinkimo tangentą: uždelsimo laikas Tu = 60 s, kompensavimo laikas Tg = 300 s. Valdymo proceso perdavimo koeficientas gaunamas faktinės vertės pokytį padalijus iš išėjimo žingsnio.
22 lygtis
Vadovaujantis nykščio taisyklėmis, gaunami tokie trikdžių elgsenos parametrai:
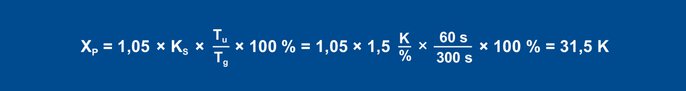
23 lygtis
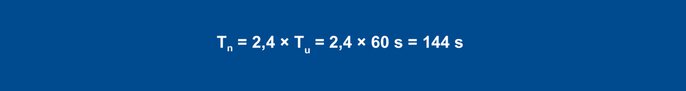
24 lygtis
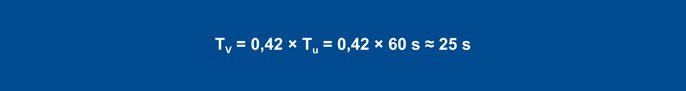
25 lygtis
Išvesties žingsnis turi būti atliekamas vėlesnio darbo taško srityje. Be to, žingsnio dydis turi būti nustatytas pakankamai didelis, kad būtų galima analizuoti faktinės vertės eigą. Nustačius išvesties žingsnį, reikia laukti tikrosios vertės pabaigos. Alternatyva, taupanti laiką, yra metodas pagal kilimo greitį.
Metodas pagal kilimo greitį
Kalbant apie žingsnio pokyčio specifikaciją, taikoma tokia pati procedūra kaip ir taikant metodą pagal proceso žingsnio atsaką. Prieš keičiant žingsnį nurodomas išėjimo lygis, dėl kurio faktinė vertė yra šiek tiek mažesnė už vėliau naudojamą nustatytąją vertę.
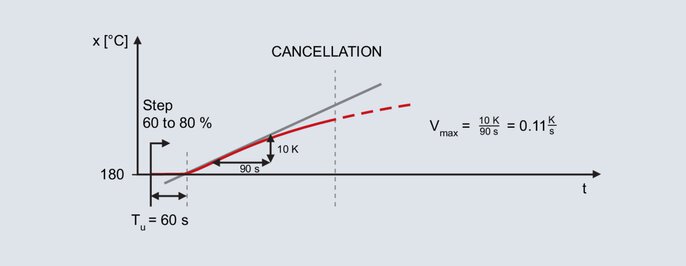
Metodo faktinės vertės kreivė pagal sūkių dažnį
Pakopos pokytis dar kartą nurodomas jau minėtai laboratorinei krosniai, kurioje vėlesnis darbinis taškas taip pat yra 200 °C. Nustačius 60 % išėjimo lygį rankiniu režimu, faktinė vertė yra 180 °C. Išėjimo lygis staiga padidinamas iki 80 %.
Nustačius pakopinį pokytį, faktinė vertė po kurio laiko padidėja. Įrašymas tęsiamas tol, kol faktinė vertė pasiekia didžiausią nuolydį. Šiuo metodu taip pat braižomas išlinkimo tangentas ir nustatomas uždelsimo laikas. Antrasis apibūdinantis parametras yra didžiausias didėjimo greitis, kuris atitinka infleksinio tangento nuolydį. Didžiausiąjį kilimo greitį galima nustatyti taikant išlinkimo tangentės nuolydžio trikampį:
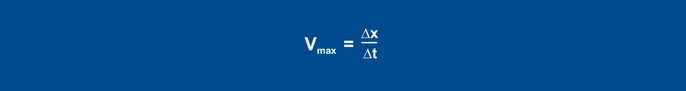
26 lygtis
Apskaičiuotos Vmax (0,11 K/s) ir Tu (60 s) vertės naudojamos šiose formulėse:
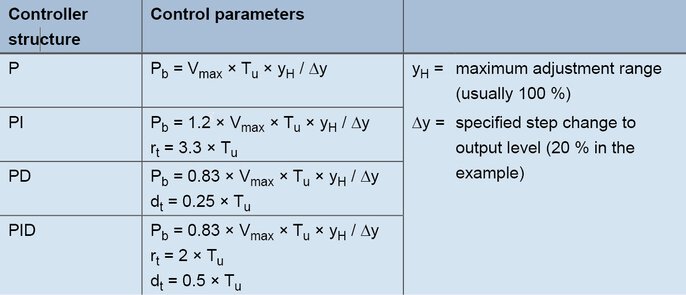
Nustatymo pagal kilimo greitį formulės
PID valdikliui pagal formules gaunamos šios reikšmės:
27 lygtis
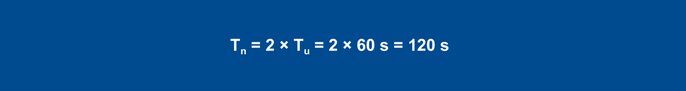
28 lygtis
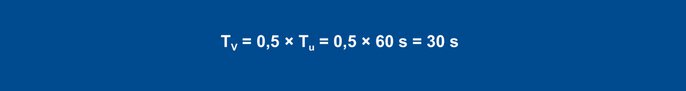
29 lygtis
Empirinis kontrolės parametrų skaičiavimo metodas
Šiuo metodu paeiliui apskaičiuojami optimalūs P, D ir I komponentų nustatymai. Pradedant nuo pradinės būsenos (0 % išėjimo lygis), kiekvieną kartą nurodoma tipinė užduotosios vertės reikšmė; todėl šis metodas tinka tik santykinai greitiems valdymo procesams (pavyzdžiui, greitiems temperatūros valdymo procesams arba tokiems valdymo kintamiesiems kaip greitis ar srautas).
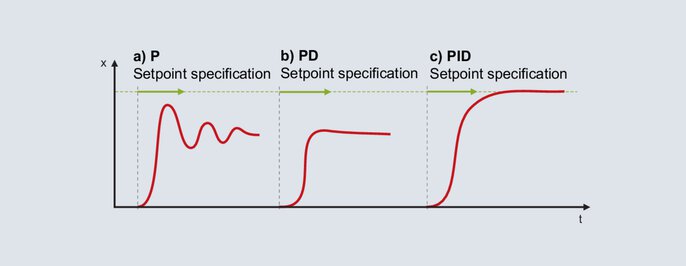
PID valdiklio nustatymas pagal empirinį metodą
Valdikliui įjungiama P struktūra. Nustatoma santykinai didelė proporcinė juosta (matmenų nustatymas priklauso nuo valdymo proceso) ir nurodoma užduotoji vertė tolesniame darbiniame diapazone. Faktinė vertė lėtai juda link galutinės vertės ir susidaro santykinai didelis valdymo nuokrypis. Tuomet užduotoji vertė nurodoma su vis mažesne proporcine juosta Pb. Siekiama, kad Pb būtų tokia, kad faktinė vertė pasiektų stabilią galutinę vertę po 2-3 visiškų svyravimų (56a pav.). Kad paleidimas būtų sklandus, struktūrą reikia perjungti iš P į PD. Pradedant nuo mažo išvestinės laiko nustatymo, užduotoji vertė nurodoma su vis didesniu dt. Jei faktinė vertė pasiekia galutinę vertę su kuo mažesniais svyravimais, dt yra optimalus nustatymas (56b pav.).
Pastaba: kai tik valdiklis net ir vieną kartą paleidimo metu nustato 0 % išėjimo lygį, tai reiškia, kad dt nustatytas per didelis.
I komponentas įjungiamas, kai struktūra perjungiama į PID. Optimalus atstatymo laikas rt paprastai nustatomas 4 kartus didesnis už anksčiau nustatytą dt vertę. 56c paveiksle parodytas atsakas, kai nustatytas rt = 4 × dt.
Kai kuriuose procesuose neįmanoma įjungti visų komponentų. Jei, naudojant P struktūrą, jau gaunamas nenustatytas atsakas su dideliu Pb, nebus galima naudoti P arba D struktūros. Vietoj to reikia naudoti I valdiklį.
Jei P valdiklis buvo sėkmingai suderintas, tačiau įvedus D komponentę valdymo kontūras tampa nestabilus, naudojama PI struktūra.
Taikant vieną iš šiame skyriuje aprašytų derinimo metodų, greičiausiai bus gautas stabilus, bet ne optimalus valdymo atsakas. Valdymo rezultatą galima dar labiau pagerinti rankiniu perreguliavimu. Jei PID valdiklio atsaką galima suderinti su viena iš 62b-62e kreivių, čia rasite informacijos apie tolesnį derinimą.
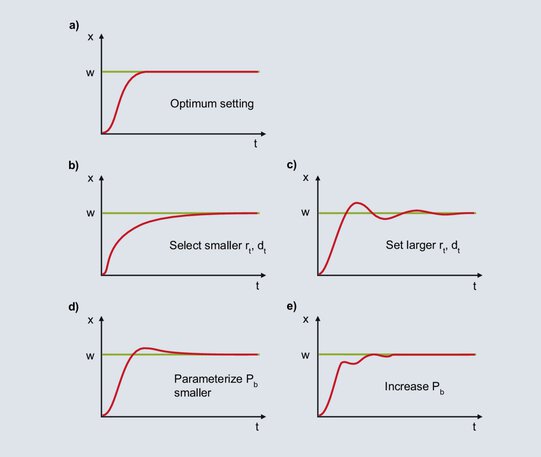
62 pav.: Pastabos dėl PID valdiklio derinimo po derinimo
Diagramoje parodyta optimali PID valdiklio elgsena.
Nustačius užduotąją vertę, faktinė vertė staigiai didėja, kol pasiekia proporcinę juostą. Jei faktinė vertė patenka į proporcinę juostą, P komponentė sumažinama, o I komponentė užtikrina, kad vertė būtų sureguliuota pagal užduotąją vertę. I komponentės didėjimas vyksta lėtai dėl santykinai didelio rt ir valdymo nuokrypis šalinamas lėtai. Norint greičiau integruoti, reikia nustatyti mažesnį rt; dt taip pat mažinamas pagal santykį dt/rt = 1/4.
Kai faktinė vertė patenka į proporcinę juostą, I komponentė padidina išėjimo lygį. Didėjimas tęsiasi tol, kol faktinė vertė pasiekia užduotąją vertę. Parodytame pavyzdyje I komponentė didina per didelį išėjimo lygį, kol panaikinamas valdymo nuokrypis, o faktinė vertė viršija užduotąją vertę. Jei yra neigiamas valdymo nuokrypis, išėjimo lygis per greitai sumažėja ir faktinė vertė nukrenta žemiau užduotosios vertės, ir t. t. Simetriškas faktinės vertės svyravimas aplink užduotąją vertę rodo, kad rt yra per mažas. rt turi būti padidintas, o dt taip pat padidintas pagal santykį dt / rt = 1/4.
I komponentė susidaro nuo to momento, kai faktinė vertė patenka į proporcinę juostą, iki valdymo nuokrypio pašalinimo. Dėl didelio Pb I komponentė jau pradeda formuoti savo išėjimo lygį, kai yra didelis valdymo nuokrypis. Dėl didelio valdymo nuokrypio pradžioje I komponentė palyginti greitai suformuoja savo išėjimo lygį. Kai valdymo nuokrypis panaikinamas, I komponentė yra per didelė ir faktinė vertė viršija užduotąją vertę. Esant mažesniam Pb nustatymui, jei yra mažesni valdymo nuokrypiai, I komponentė pradeda formuoti savo išėjimo lygį atitinkamai lėčiau. Pavaizduotas vienkartinis viršijimas tampa labiau neįtikėtinas.
Nustačius per mažą Pb reikšmę, P komponento išėjimo lygis sumažėja netrukus prieš pasiekiant užduotąją vertę. Tikrajai vertei patekus į proporcinę sritį, P komponentė smarkiai sumažėja, o tikroji vertė sumažėja. Dėl didesnio valdymo nuokrypio išėjimo lygis tampa didesnis, o faktinė vertė padidėja. Proporcinėje juostoje maži faktinės vertės pokyčiai lemia didelius išėjimo lygio pokyčius, todėl atsiranda didelė svyravimo tendencija. Tai nuraminama didinant proporcinę juostą.
